参考文献
[1]GB/T 23935-2009,圆柱螺旋弹簧设计计算
[2]机械设计手册 第六版 第2卷,秦大同、谢里阳 主编,化学工业出版社
一般所说的弹簧是指圆截面材料、圆柱螺旋弹簧,是弹簧中非常常用的一种。弹簧还有很多其他形制,可以参考设计手册。
一、基本参数
基本外形参数
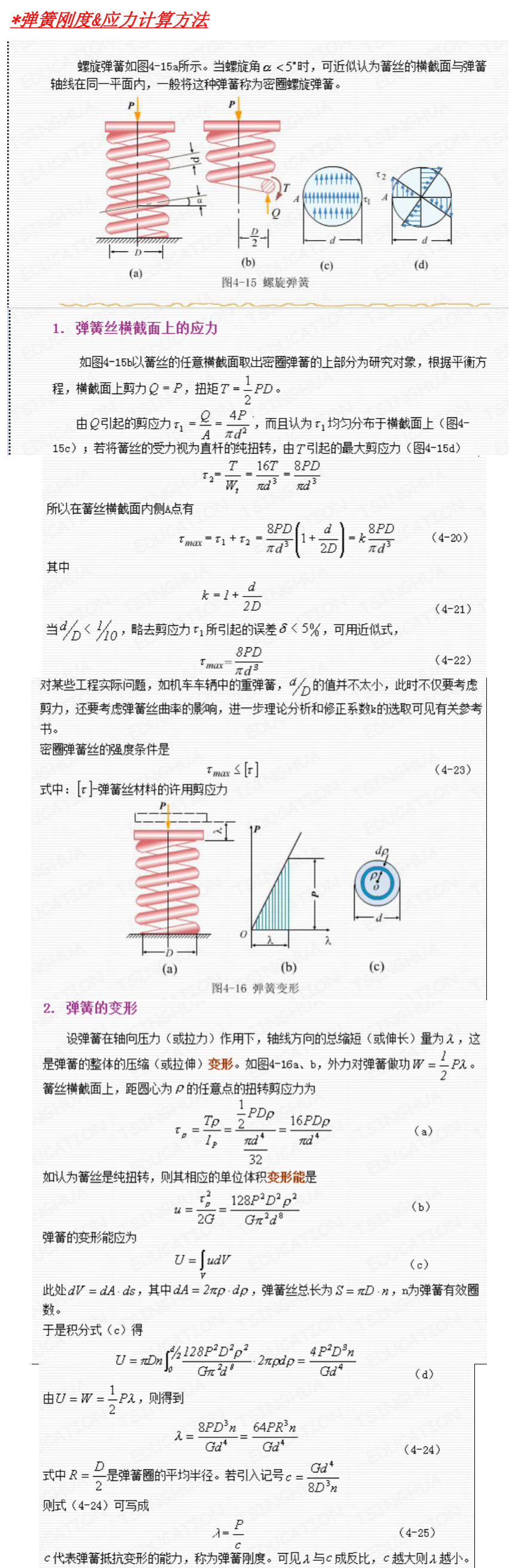
通过这几个参数可以基本确定弹簧的形状
1.线径$d$
弹簧钢丝的直径
2.外径$D_2$,中径$D$,内径$D_1$
这三个参数实际上是一个东西,表示绕成的圆柱外形的直径是多少,三者之间可以互相转化
$D=D_2-d=D_1+d$
注意是直径不是半径
一般公式中用的是中径,淘宝上卖的多用外径
3.节距$t$和间距,表示绕的密度
节距$t$:指绕制后两圈钢丝中心的距离
间距$\delta$:两个钢丝外边空隙的距离
$\delta=t-d$
4.总圈数$n_1$、支承圈数$n_2$、有效圈数$n$
弹簧绕了几圈,和弹簧原始长度$H_0$大致有关系
$H_0=nt$
考虑到端部型制,可能还有比较特殊的几圈,称为支承圈,因此并不精确,具体见下文
$n_1=n+n_2$
力学参数
1.刚度(国标符号$F'$,也用$k$)
表示力和位移之间的关系,即$F=k\Delta x$
刚度k越大,相同变形$\Delta x$需要的力越大、越难拉伸,和名字中的“刚”是相对应的
刚度(多圈刚度)$k=\frac{Gd^4}{n8D^3}$
G:材料的剪切模量,一般计算可以取75Gpa,特殊材料查表或做试验
n:有效圈数,见下文
这实际是多圈合并计算的刚度,我们可以定义一个单圈刚度$k_1$
$k_1=\frac{Gd^4}{8D^3}$
单圈刚度比多圈刚度大,因为多圈串联以后力不变,但位移变成了n倍
刚度公式推导可参考材料力学相关书籍,我在最后附了我找到的一份ppt截图可以参考,出处已经找不到了
2.变形$f$
即$\Delta x$,相比原始长度$H_0$的变化量
$f=H-H_0$
单圈变形$f_1=f/n$
3.负荷$F$
负载、受力
注:弹簧多圈之间受力是一样的,不存在单圈受力和多圈受力的说法
4. 应力
弹簧所受为剪应力
$\tau=K\frac{8DF}{\pi d^3}$
K为曲度系数,见下文
F为当前受力
利用刚度公式,还可以把它转化为
$\tau=K\frac{Gdf}{\pi D^2n}$
应力主要用来验算弹簧会不会断掉或者因为各种其他原因而不能工作
极限应力大小$[\tau]$根据手册选取,和材料的极限抗拉强度$\sigma_b$不同,需要考虑到各种因素,如卷曲引起的局部应力集中和疲劳的循环特性
我计算中用的是200Mpa,也可以500Mpa,1000Mpa
其他辅助参数
1.旋绕比$C=\frac{D}{d}$
2.曲度系数$K=\frac{4C-1}{4C-4}+\frac{0.615}{C}$
这两个参数用来修正一些应力的公式
3.高径比$b$
用来校验稳定性,防止弹簧太长受压侧向失稳,具体参考设计手册10-32
4.螺旋角$\alpha=\text{arctan}\frac{t}{\pi D}$
还有很多参数,要求不高的话用不到,这里不一一列举了。
一些严格要求的弹簧还有一些校验,比如弹簧压并后的横向变大等等,具体参考手册
二、选型
1.根据设计要求进行反推计算
首先确认自己的设计要求,如果自己做东西范围比较宽,那就先随便算几个
比如说$\Delta x$=10mm,F=1~10N,就能确定刚度k的范围
然后根据设计手册的表格的单圈变形和单圈刚度选择线径和中径
然后确定圈数、长度等参数,再去找店家有没有参数,没有也可以定制
整个过程主要是要反复迭代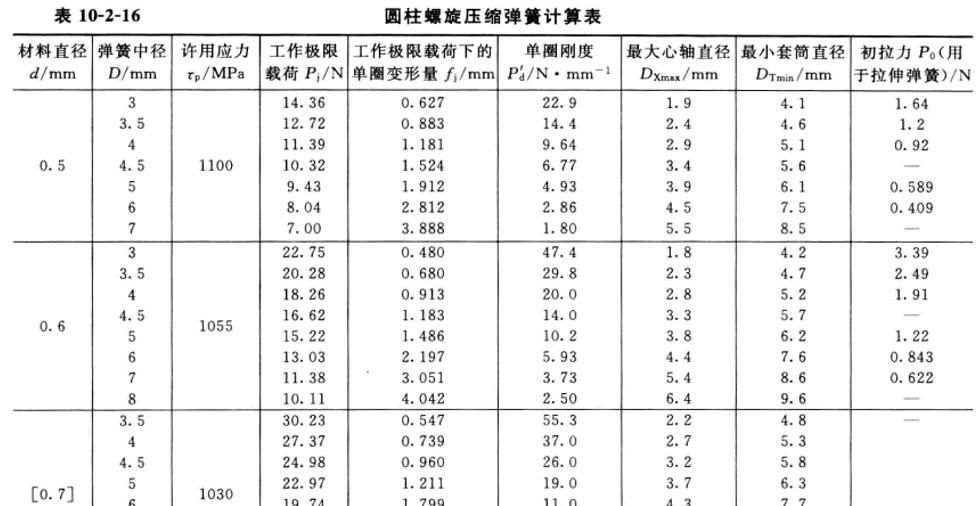
这部分之前一次选型的笔记丢了,有机会再详细写
2.根据商家已有尺寸参数进行选型
计算时较方便,都是带入公式正向计算。
算完后也不会找不到型号,缺点是型号有限
a)压缩弹簧
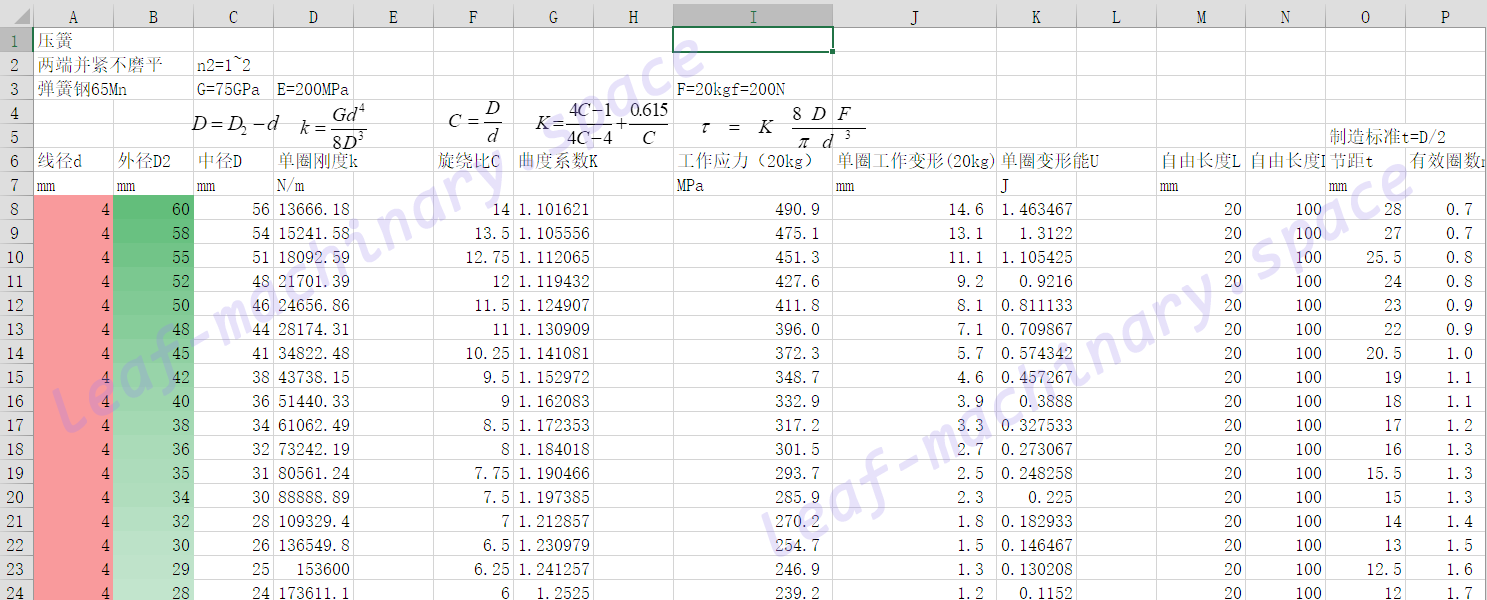
这是淘宝上某个商家的压缩弹簧参数表格,这些参数不需要额外定制,因此非常便宜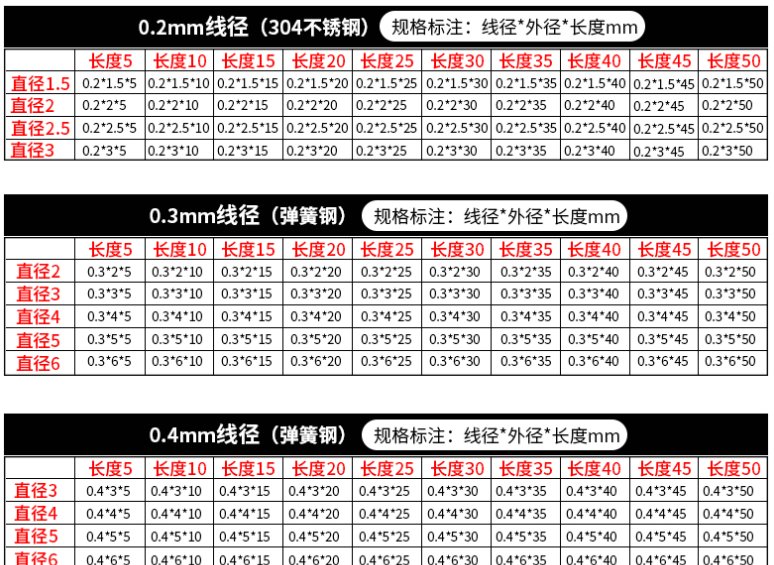
但是需要注意的一点是少了关于节距/圈数的信息,因此必须问客服要到这一关键信息。下面这家店是我软磨硬泡问出来的(不是广告,没有收广告费)。
有了这些信息之后,就可以开心的选型了。我用excel做的计算表是这样的,算完了排个序什么的随便弄
这是表格的下载
b)拉伸弹簧
对于拉伸弹簧来说,要简单的多,因为大部分都是密绕弹簧,也就是说每两圈之间没有空隙,那么节距t就等于线径d。也可能要考虑初拉力的问题,不过影响不大。
计算表是相似的。但是要注意去掉长度里面两边拉环的长度,才是实际有效的弹簧部分
下面实测数据用的是拉力计,单位是kg,相差不是很大。同时数弹簧的圈数也发现和计算结果相符合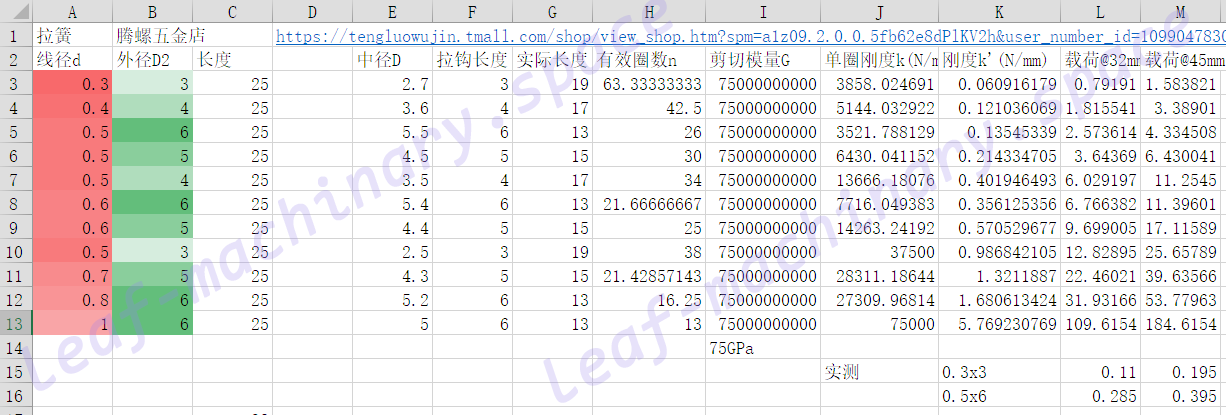
c)扭转弹簧
扭转弹簧没用过,公式不一样,这里先留个坑
三、弹簧刚度公式推导
这个图片是好久前从网上某个ppt摘到笔记里的,现在已经找不到出处了,仅供参考